こんにちは、りんどばーぐです。やや久しぶりのヒトツマミ執筆でございます。
今期ヒトツマミ編集部の編集長になりました。
新入生も入りまして、多くの投稿をお届けしていこうかなと思っております。お楽しみに。
さて、この度私、あることを考えたのです。
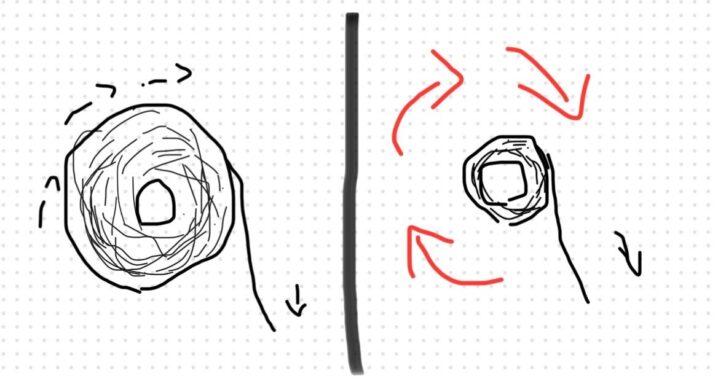
私はよくトイレで大をするときにはめいっぱいトイレットペーパーを使うのですが、あれって使い始めはゆっくり減るけど、残り少なくなってくると急になくなりますよね?
・・・・・・・
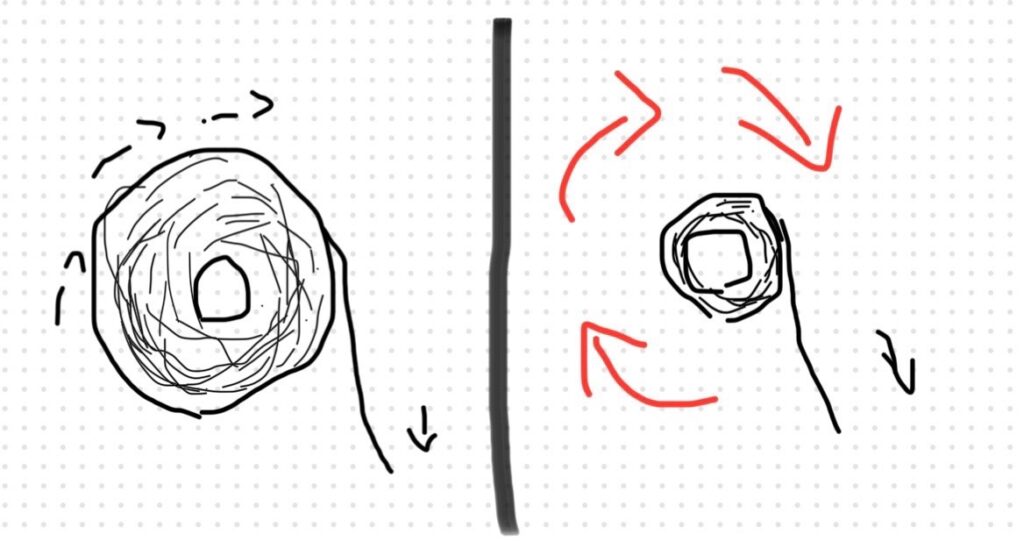
??もしかして加速度的に減っていくのでしょうか・・・?
なんかの関数で表せるのでは?と思いまして、超数弱な筆者がちょっと計算を試みました。
トイレットペーパーの図形量
まずはトイレットペーパーの図形量を定義してみましょう!
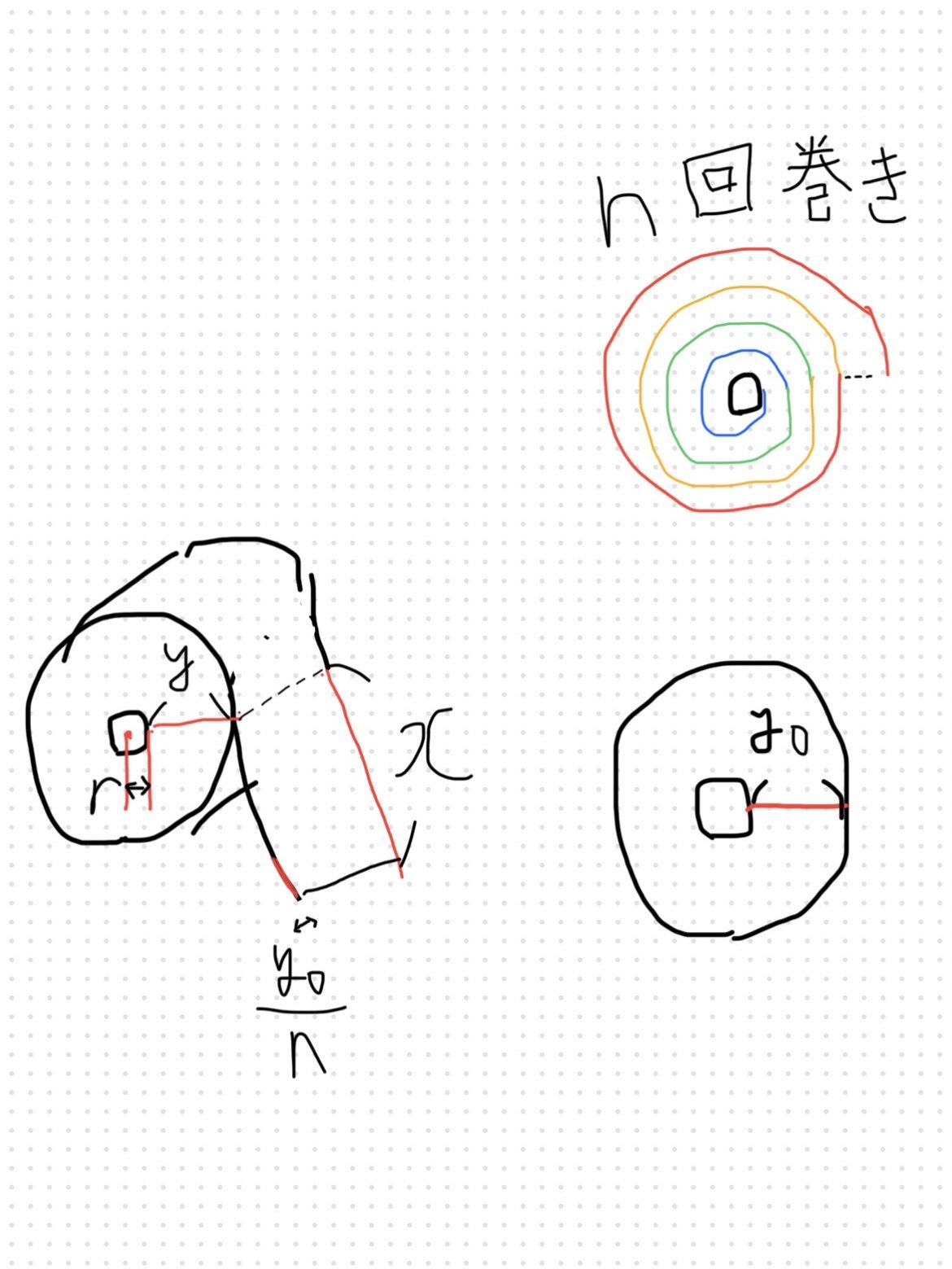
まず、この関数で求めたい変数を設定します。
\(x\):トイレットペーパーの使った部分の長さ
\(y\):芯の外周からトイレットペーパーの外周までの距離(トイレットペーパーが重なってる部分の厚み)
続いて定数を設定します。
\(r\):芯の半径
\( y_0 \):初期状態(\( x = 0 \)のとき)の\(y\)
\( n \):紙が巻かれている回数
\( \frac{y₀}{n} \):トイレットペーパー1枚分の厚さ
芯の厚さ:\(0\)
トイレットペーパーが巻かれている部分の形状は常に円
以上のように仮定します。
計算タイム
では、ここからどのように関数を決定すればよいのでしょうか・・・?
筆者はよくわからないながらもすこ~し計算してみました。
まず、トイレットペーパーを初期状態から1周巻き取ってみます。
このときの\(x\)は初期状態の円周ですから、\(x\)は\( 2\pi(r+y₀) \)増加します。
そしてこのとき、\(y\)はトイレットペーパー1枚の厚さ分、つまり\( \frac{y₀}{n} \)減少しますね。
もう1回巻き取ってみましょう。
2回目に追加的に巻き取る長さ\(x\)は1回巻き終わった後の円周分ですから、\(2\pi\left(r+y₀-\frac{y₀}{n}\right)=2\pi\left(r+\frac{y₀(n-1)}{n}\right)\)増加します。
このときも\(y\)は\( \frac{y₀}{n} \)減少しますね。
3回目も同様に、
\(x\)がさらに\(2\pi\left(r+y₀-2\frac{y₀}{n}\right)=2\pi\left(r+\frac{y₀(n-2)}{n}\right)\)増加し
\(y\)は\( \frac{y₀}{n} \)減少します。
よって、トイレットペーパーを\(n\)回(全部)巻き取った場合、
\(x\)が初期状態から累計で\(\sum_{k=1}^{n} 2\pi\left(r+\frac{y₀}{n}(n-k+1)\right)\)増加すると、\(y\)が\( y_0 \)減少して\( y = 0 \)となります。
・・・・・だから何なのでしょう。?
筆者にはここからどうしてよいか全くわかりませんでした。
これが入試問題だったら部分点で1割くらいもらえるかしら?
完全にお手上げなのでChat GPTさんに聞いてみました!
Chat GPTさんがんばりタイム

さあ、どうなる???

出ました、計算結果。
\( y = r + \frac{y_0}{n} \left( n – \frac{x}{2\pi\left( r + \frac{y_0}{2n}(m-1) \right)} \right) \)
・・・・・・あってるのか??
しかし、勝手に定義された定数\(m\)が残ったままですね。これは消去してもらいましょう。

\( y = y_0 – \frac{y_0 \cdot x}{2 \pi n \left( r + \frac{y_0}{2n} \left( \frac{y_0 \cdot x}{2 \pi n r + \frac{y_0^2 x}{4 \pi n^2}} – 1 \right) \right)} \)
だいぶ複雑になりました。
グラフを書くとどうなっているのでしょうか???
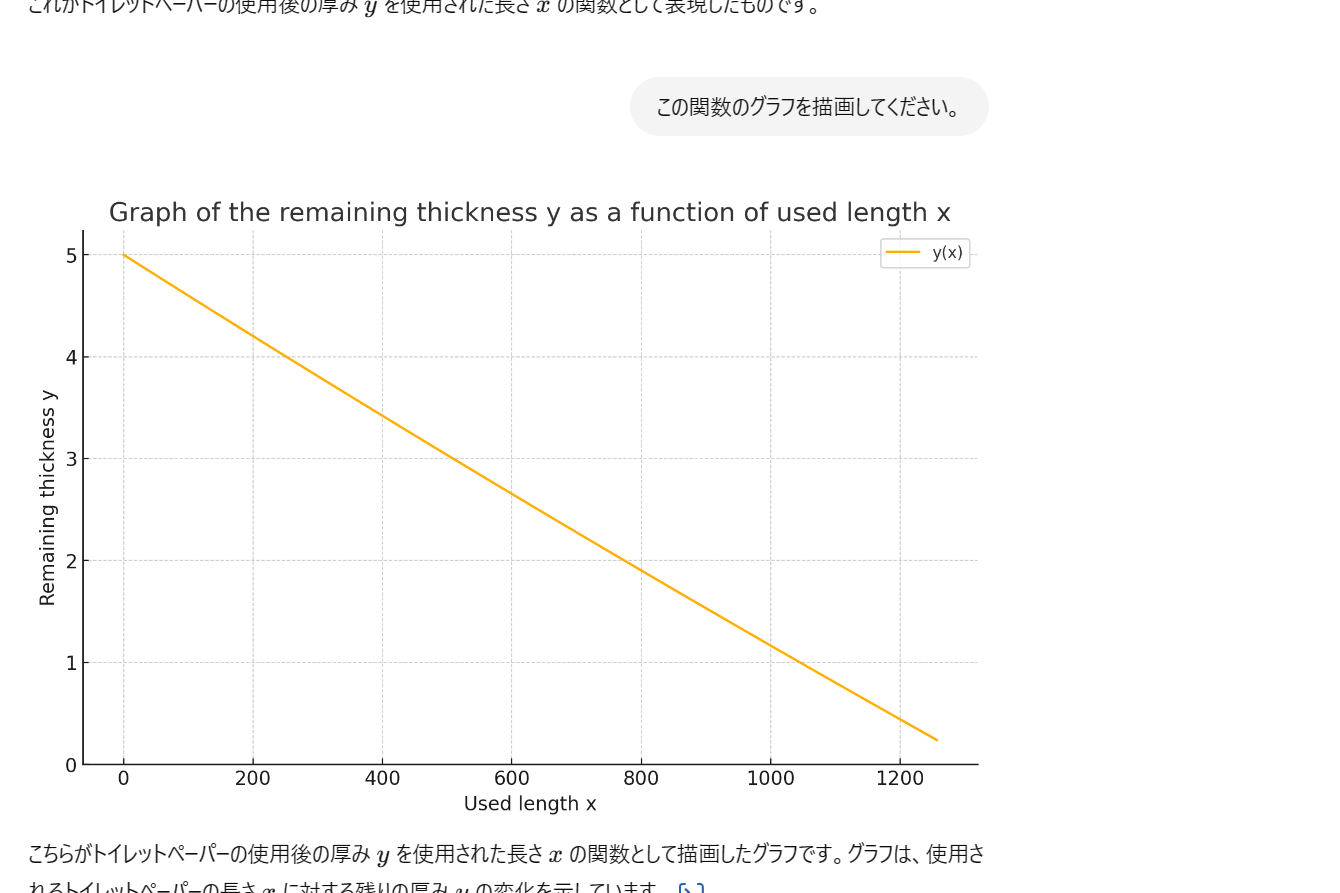
・・・・・・??????????
うーん、思ってたのと違うなあ、普通の1次関数のように見えますね。
トイレットペーパーの減り方の挙動に合わないと思われるので、もう1回。
Chat GPTさん泣きの1回



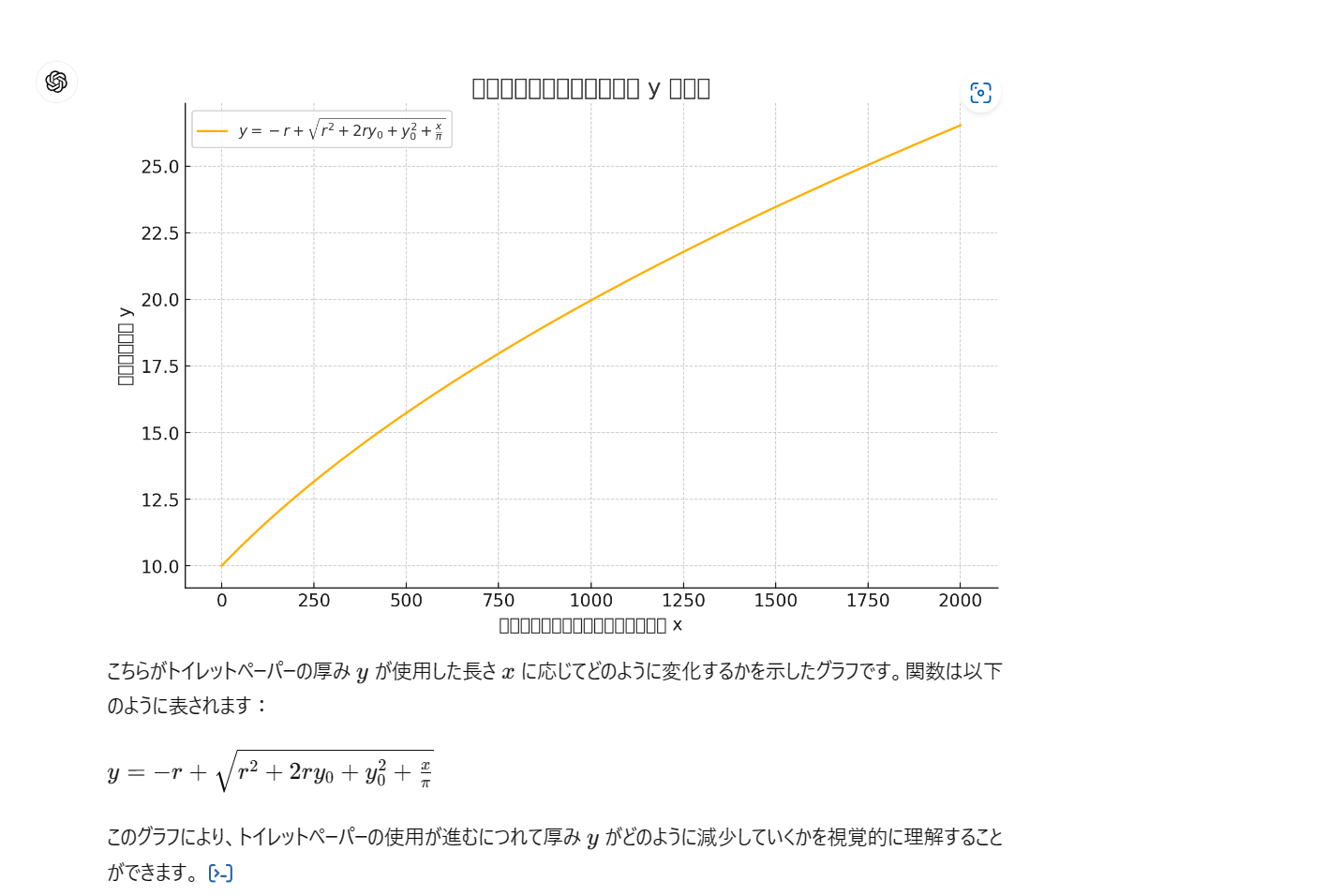
・・・・・・まさかの単調増加!?\(◎o◎)/!
結構スリムな式になっていい感じかと思ったのに、、、
なので、「減少関数になるはずですが…」とオーダーしたところ、、、

ん、さっきのやつの\(\frac{x}{\pi}\)の符号だけ変えたやつが出てきましたね。
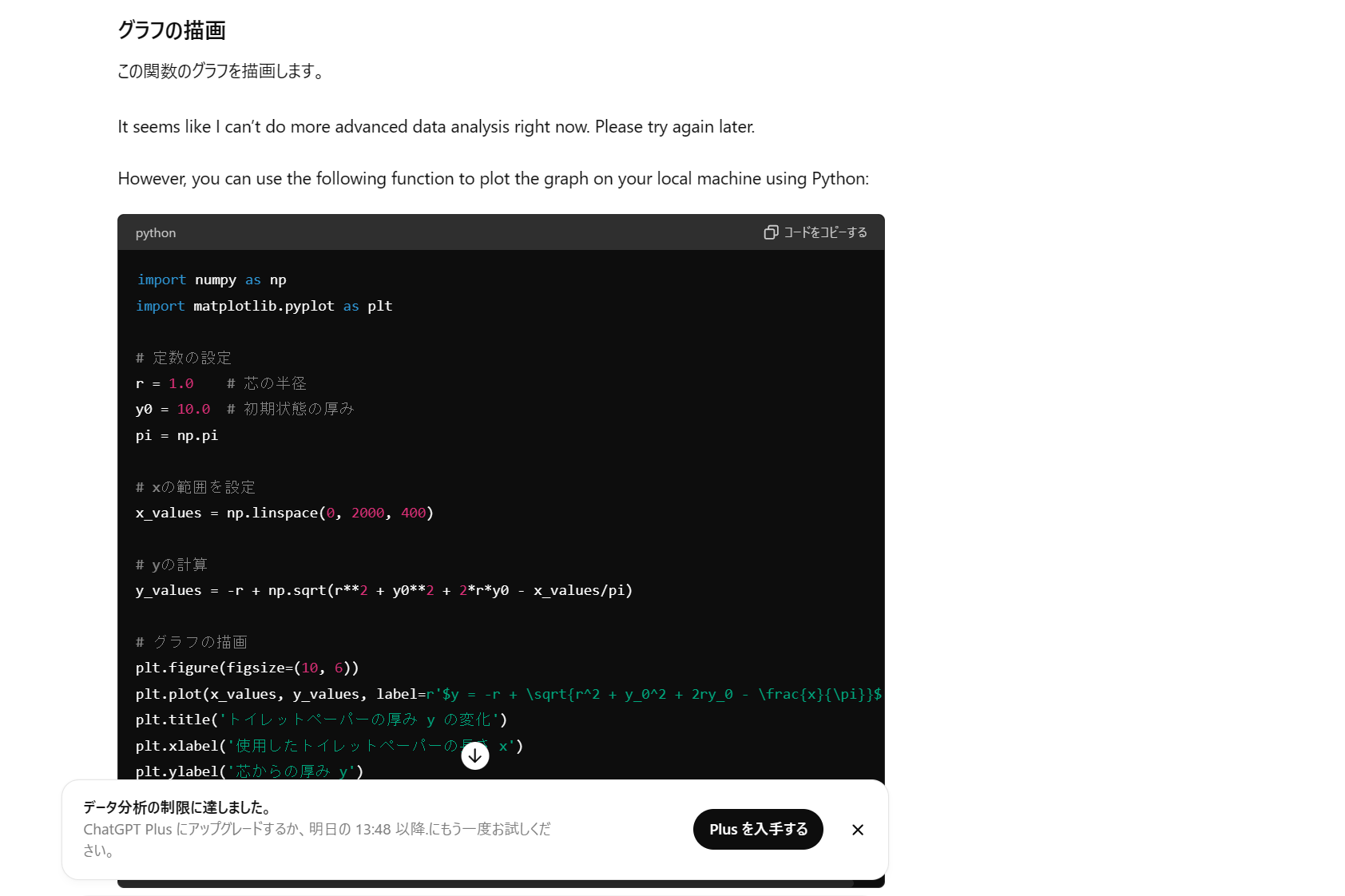
ただ、グラフを書いてもらおうとすると力尽きたみたいで、コードだけ置いて帰っちゃいました。
コードをコピーしてGoogle Colaboratoryに貼り付けると・・・?
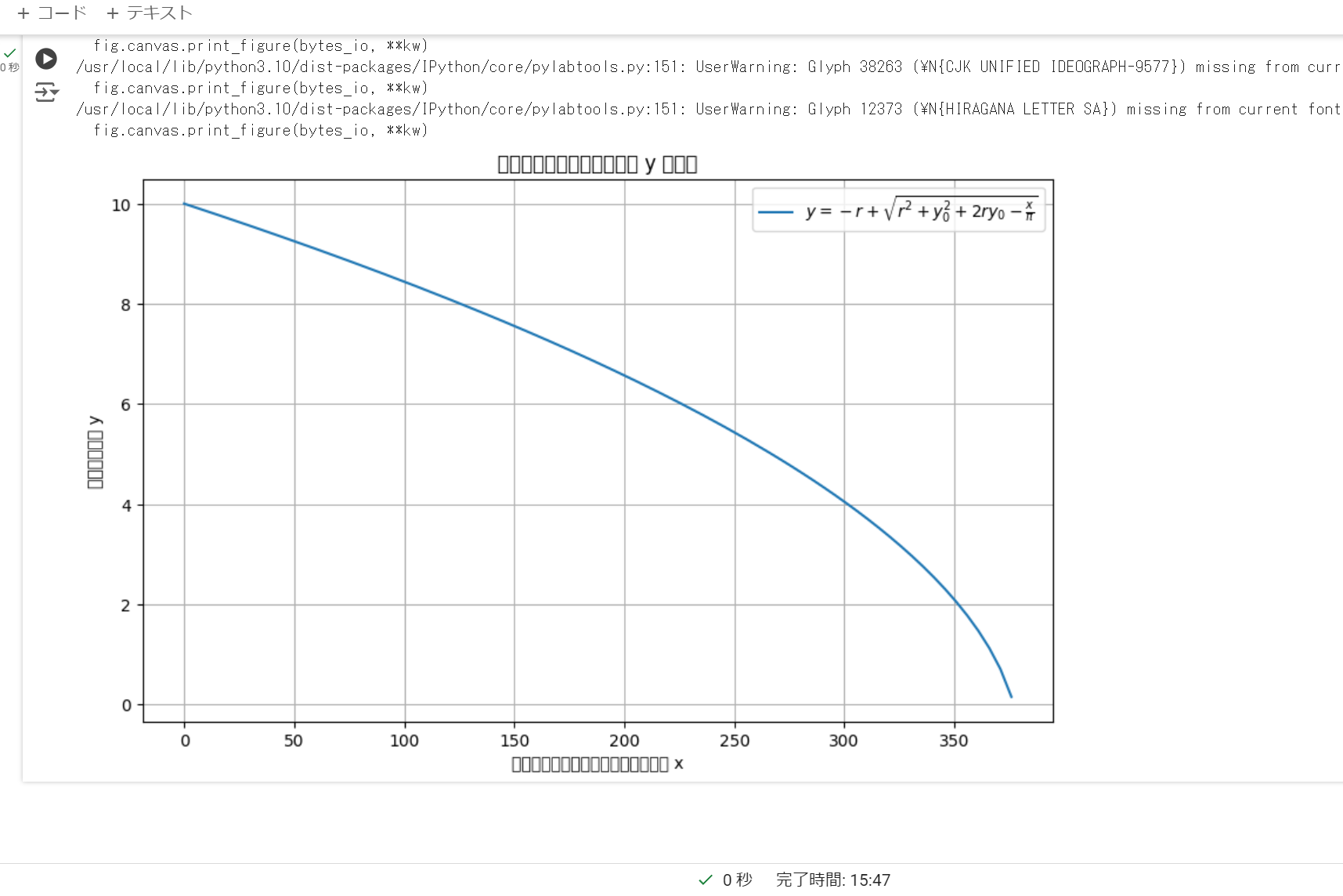
!!!!!
なんか合ってそう!!!!
残り少なくなるにつれて急激に減っていく様子がみてとれますね。
まあ、筆者には計算のプロセスも結果が合ってるのかどうかも、まるっきり分からないのですが。。。
まとめ
以上のように、トイレットペーパーを\(x\)使った時の残りのトイレットペーパーが重なってる部分の厚み\(y\)は
\( y = -r + \sqrt{r^2 + y_0^2 + 2ry_0 – \frac{x}{\pi}} \)
と表されるようです。真偽はわかりません。ぜひお手元のトイレットペーパーで実験してみてください。
改善すべき点がございましたら、お近くのHASC部員まで。