私はこれを「プロ数学ング」と名付けたいと思ってる……!
居酒屋で酒を飲みすぎて気分がよくなったたじパン(2022年3月25日)
こんにちは、一橋大好きマン(笑)のたじたじパンジーです。
突然ですが、ヒトツマミ読者の皆さんならもう、本学にデータサイエンス学部が設置されることはご存じですね?
来年の4月に開学されるらしいので来年度にはデータサイエンス学部の受験生が一橋にやってくるというわけです。わくわくするね!
しかしそこでたじパン、一つの疑問が浮かびます。
ベロベロなたじパン「せっかく尖った名前の学部を作るんだ、問題も独自に尖ってくれないとなぁ???」
素面なうのたじパン「(そんなことできるわけないだろ……)」
というわけで今回は、「来年はまあ無理として今後プログラミングで数学を解く入試問題が出るといいな!」という希望的観測により、一橋の数学を数学とプログラミングの併用で解いていこうと思います!
ルール説明
さて、こうして始まった「プロ数学ング」なのですが、当然ながら誰も先駆者がいないのでルールなどは特に決まっていません。そこで、私たじパンが勝手にルールを作ってみました!
一橋プロ数学ングのルール
- 得点(部分点でも可)できた部分のうち、半分以上がプログラミングによる導出となっていること。
- 同じ大問、小問内で数学とプログラミング両方を使っても構わない。
- プログラミング言語は自由。ただし特定のプログラムを実装するコードをネットで検索してはいけない(関数の仕様確認はOK)。
- 試験時間は本番と同じ。
- 経済・商学部は3完、法・社会学部は2完を合格の条件とする。
いかがでしょうか。我ながら良い出来だと思うんですが、もし問題点とかあれば直すかもです。……次があれば。
もしこのルールで遊んだ方がいましたらぜひお近くのヒトツマミライターにお声がけください!人づてに話を聞いたたじパンが嬉し泣きします。
さて、そんなこんなでルール決めも終わったので、問題をやっていきますかー!えいえいおー!
問題を解く
その前に
早速問題を解いていくのですが、解きながら思ったことがあります。
これ、受験生の皆さんにとって、実際の一橋生が数学を解くときの視点を見られるあんまりない機会だと思います。
私はお世辞にも余裕で受かったわけではありませんが、それでも十二分に対策して受けた(つもり)(本番1完半)なので、ぜひ参考にしてみてください。
回答開始
俯瞰する
さて、まずは問題を眺めてみます。
(皆さんもここから問題PDFを見られますよ)
うーん。とりあえず大問1はカモですね。素数判定はプログラミングを勉強していると練習問題などでよく見かけるので、まずこれはプログラミングで解きましょう。
大問2はよくわからんなあ。2の指数だけ変わる群数列になるようだけど、一般項の導出が思いつかないし、それが分からないと和もキツそうだな……保留。
大問3は(1)が簡単そう。多分解と係数の関係でなんやかんやしたら上手いこと行くやつだよね。範囲を与えることになる条件も恐らく三角形の存在条件のあの不等式でしょう。複数の不等式を解くにはプログラミングは不向きなので、ここは数学で行きましょう。
大問4はカモ2ですね。円と放物線が与えられて共有点3つは分かりやすいなあ。(1)は有限個の解を求めればよいらしいのでプログラミングの出番です。(2)は……ひとまず何を言っているのかよく分からないので保留で。
大問5はカモ3ですね。先ほども言いましたが有限個の数字をいじるのはプログラミングが得意としていることです。問題も定積分の確率なのでプログラミングで問題ないでしょう。
総括するとプログラミング2完半と数学0.5完ですね。私は経済学部なので、合計3完はちょうどいいのですが、減点も見越してもう少し稼ぎたいところ。
大問1 整数問題

この大問は素数を判定するプログラミングを実装すれば終わりなので、大して苦労はしないでしょう。すらすら書いていきます。言語は数学的な計算もできるPythonを選択しました。
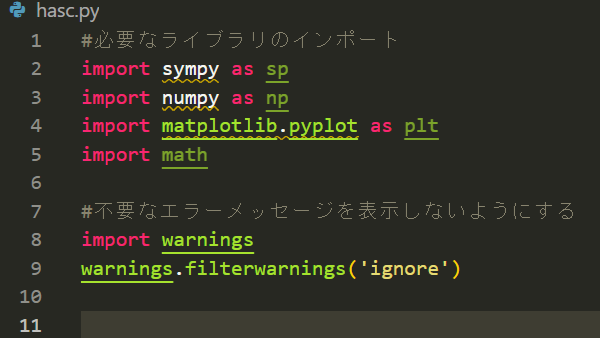
ずばり結果から言うと、こんな感じになりました。
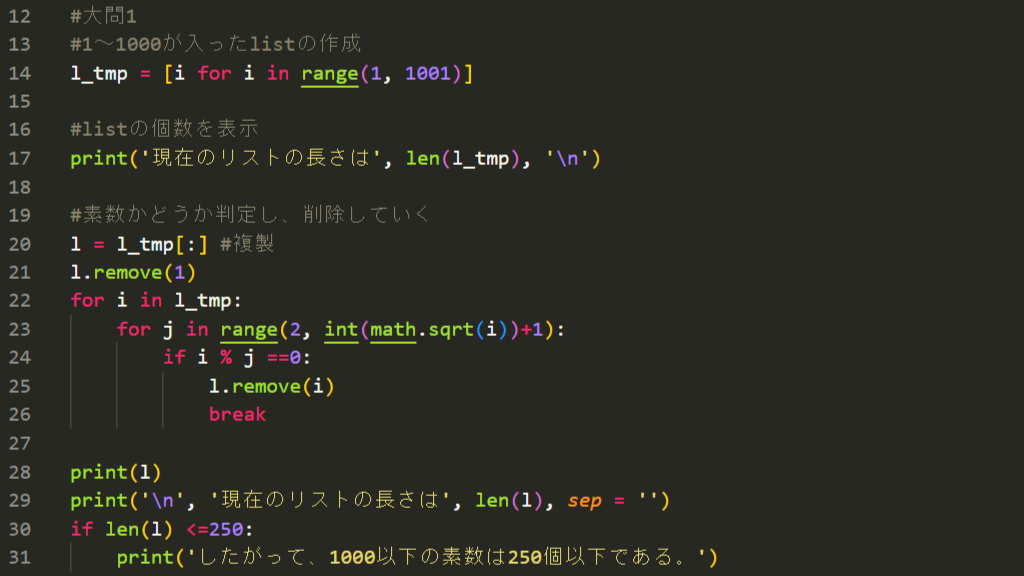
こうすると出力の最後にはこう表示されます。
| 現在のリストの長さは168 したがって、1000以下の素数は250個以下である。 |
ざっくり何をやっているのかを説明すると、
- まず1~1000の整数が入ったリストを作り
- リストのそれぞれの整数に対して約数を持っていないか確認し
- 持っていたらリストから削除する
といった感じです。最終的には素数のみが残り、それが250個以下だったので、題意は示せました。
どんどん行こう!
大問5 積分と確率

この大問ですが、積分をしているのでさっきよりは難しいです。Pythonのライブラリ(拡張機能みたいなもの)のsympyを使用します。
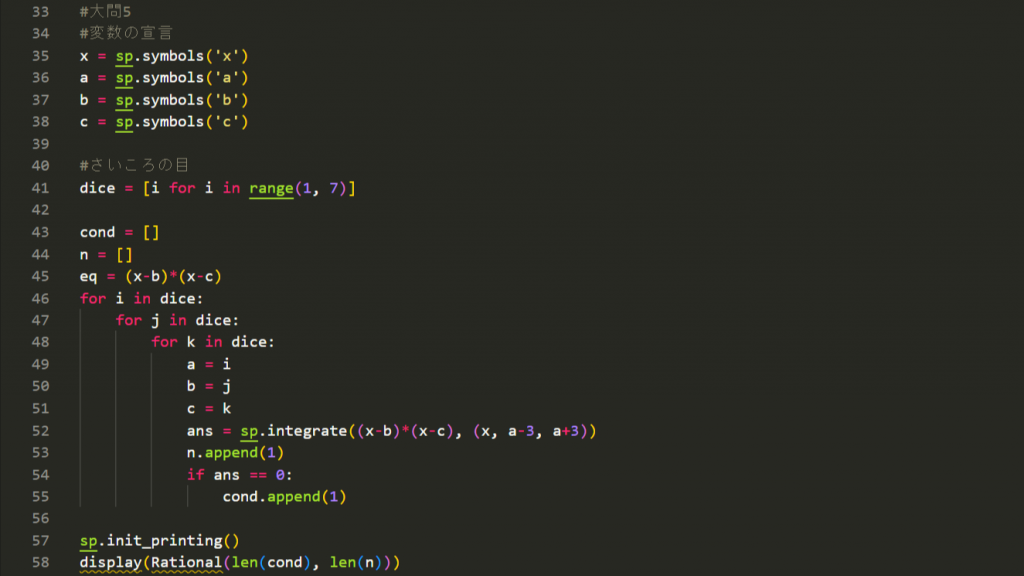
こんな感じになりました。大変お見苦しいコードなのですがざっくり説明をすると、
- さいころの目の組み合わせ1つ1つに対して
- 定積分を計算し
- 分母のカウントを+1し、更に定積分がゼロなら分子のカウントを+1する
といった感じです。事象の数が有限なので人間にはできませんが数え上げてしまえばいいだけなのです。
ちなみに答えはこんな感じ。
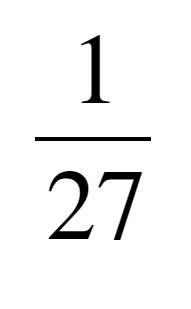
(なぜかwwwでかいんだがwww)
小休止
結構長くなってしまったので、一度ここで止めておきたいと思います。2020年度編<後>では残る問題を解いて、丸つけまでいきます。
合格できるのかどうか……乞うご期待!!!!
(なんかいけそうじゃね?)
後編はこちら














