(↑Nano Banana Pro)
受験生のみなさん、あけましておめでたい次第である。もうすぐ共通テスト(以下、通スト。2ストライクの略のツーストのイントネーションではなく、CUTIE STREETの略のキューストのイントネーション。)だが、通ストといえば、筆者は2日目の朝に蕎麦(好みの薬味ネギ大量入り)を食べ受験会場で嘔吐したという思い出がある。
今回もともと記事にしようと思っていた内容は
「北海道以外の物産展、そんなにない説」である。
読者の皆様もちょっとは感じたことがあるのではないだろうか、たまに新宿伊勢丹に入って地下行ったら・・・やってるやってる北海道物産展。
カニ・ウニ・イクラ・バター・ザンギ・じゃがいも・白い恋人・・・・
皆さんの脳内では「物産展」と聞いたら特に断らない限りこれらの物産を指すものとされているだろう。
藤井(2021)によれば、2016年に開催された物産展のうち3割超(海外除く)が北海道を対象地域として選定していた。
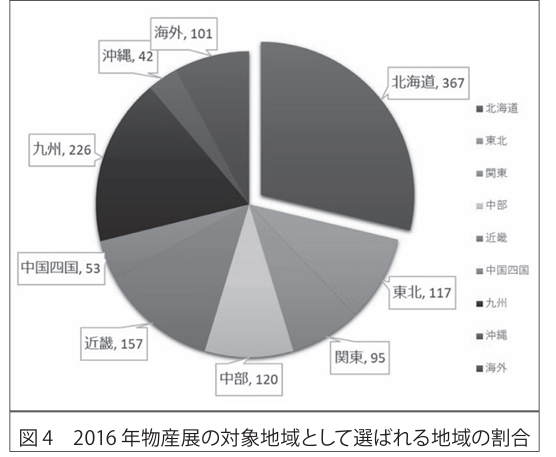
https://ycu.repo.nii.ac.jp/records/2177#
全国の農業産出額・漁業産出額のうち北海道が占める割合はそれぞれ15%弱・20%弱で推移しているにもかかわらず、この優遇ぶりには目をちょっとだけ見張るものがある。
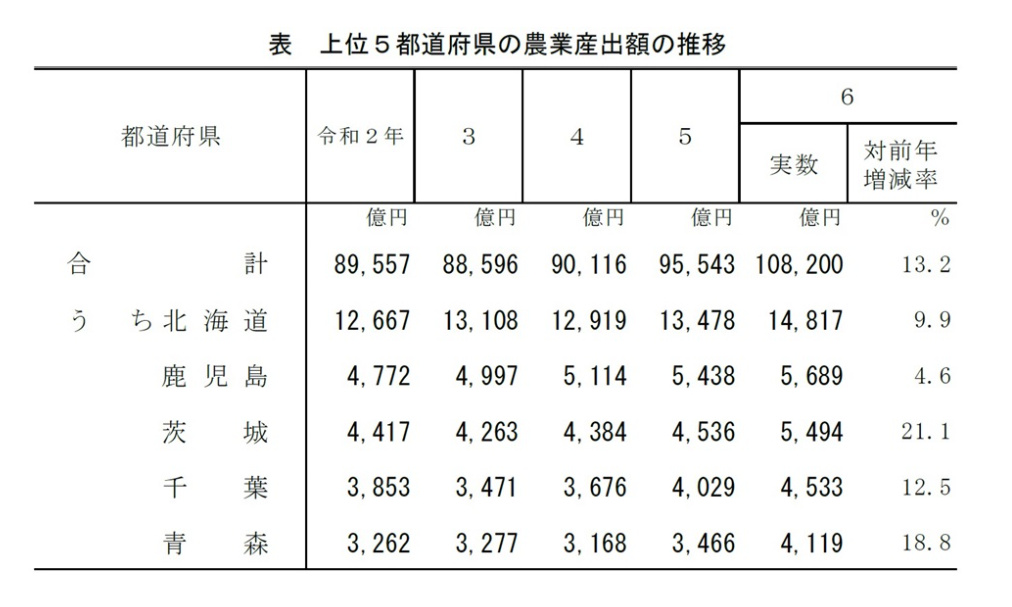
https://www.maff.go.jp/j/tokei/kekka_gaiyou/seisan_shotoku/r6_betsu/index.html
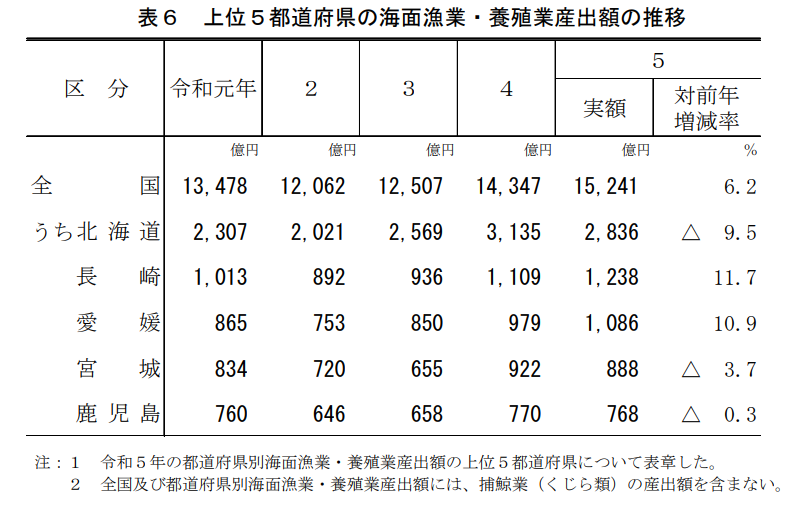
https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00500208&tstat=000001015664&cycle=7&year=20230&month=0&tclass1=000001036597&tclass2=000001227398
・・・・・北海道以外の物産展、生産額に対してそんなにないということで(?)、説立証である。
以上で記事を終わってもよかったのだが、4代目・無い内亭 円楽を襲名した私は年始に長文エントリーシートを書いていたらすっかり寝られなくなってしまい、一橋大学受験生の通スト対策の一助となればと思い、Gemini 3とおしゃべりしながら予想問題を作成する仕儀と相成った。
まず、物産展.com(https://bussan10.com/)という素晴らしいwebサイトを参照し、2025年に開催された物産展を改めて調査した。

その結果、日本全国の4つの百貨店(※1)の店舗数とそこにおいて2025年に開催された(※2)催事(※3)の総数とそのうち北海道物産展の数は下表のようになった。
※1 三越、伊勢丹、高島屋、松坂屋
※2 開催日程のうち2025年を1日でも含む
※3 多くは地域物産展だがそれに限らない
表
| 店舗数 | 催事総数 | うち北海道物産展 | |
| 三越 | 10 | 41 | 8 |
| 伊勢丹 | 6 | 60 | 14 |
| 高島屋 | 16 | 116 | 21 |
| 松坂屋 | 4 | 37 | 6 |
| 合計 | 36 | 254 | 49 |
もんだい!(平成教育委員会の声で)

百貨店好きな花子さんは、日本全国の三越・伊勢丹・高島屋・松坂屋にランダムで入店する性質を持っている。つまり、各店舗に入店することは同様に確からしい。また、各百貨店ブランドで北海道物産展が行われている確率は催事総数とそのうちの北海道物産展の数の比に従う。例えば、日本橋高島屋S.C.と高島屋大宮店で北海道物産展が開催される確率は等しく\( \frac{21}{116} \)である。
このとき、花子さんがある百貨店に入って北海道物産展が行われていたとき、そこが三越である条件付き確率を求めよ。
-----気分が変わりここから「だ・である調」→「です・ます調」-----
よくわかる解説~(平成教育委員会の声で)

条件付き確率の問題で重要なのは、(というかそこしかないが)「〇〇なとき」を構成する全事象(分母になる)をちゃんとイメージできるかですね。
この問題では、「花子さんが入った店で北海道物産展が行われている」という事象ですな。
各百貨店ブランドにおける北海道物産展開催確率を店舗の存在比で加重平均しましょう。
$$
\begin{aligned}
&\text{【① 各百貨店ブランドにおける北海道物産展開催確率】} \\
&\text{三越:} P(北|三) = \frac{8}{41}, \quad \text{伊勢丹:} P(北|伊) = \frac{14}{60} = \frac{7}{30} \\
&\text{高島屋:} P(北|高) = \frac{21}{116}, \quad \text{松坂屋:} P(北|松) = \frac{6}{31} \\
\\
&\text{【② 店舗の存在比(入店確率)】} \\
&P(三) = \frac{10}{36}, \quad P(伊) = \frac{6}{36}, \quad P(高) = \frac{16}{36}, \quad P(松) = \frac{4}{36}
\end{aligned}
$$
$$
\begin{aligned}
&\text{【③ 北海道物産展が行われている全確率 } P(北) \text{ 】} \\
P(北) &= P(三)P(北|三) + P(伊)P(北|伊) + P(高)P(北|伊) + P(松)P(北|松) \\
&= \left( \frac{10}{36} \times \frac{8}{41} \right) + \left( \frac{6}{36} \times \frac{7}{30} \right) + \left( \frac{16}{36} \times \frac{21}{116} \right) + \left( \frac{4}{36} \times \frac{6}{37} \right) \\
&= \frac{20}{369} + \frac{7}{180} + \frac{7}{87} + \frac{2}{111} \\
\\
&\text{各項を通分して整理すると:} \\
P(北) &= \frac{505657}{2639580} \quad (\approx 19.16\%)
\end{aligned}
$$
$$
\begin{aligned}
&\text{【④ 北海道物産展開催時にそこが三越である確率】} \\
P(三|北) &= \frac{P(三 \cap 北)}{P(北)} \\
&= \frac{\frac{20}{369}}{\frac{505657}{2639580}} = \frac{20}{369} \times \frac{2639580}{505657} \\
&= \frac{20 \times 3 \times 41 \times 21460}{3 \times 3 \times 41 \times 505657} = \frac{20 \times 21460}{3 \times 505657} \\
&= \mathbf{\frac{429200}{1516971} \quad (\approx 28.29\%)}
\end{aligned}
$$
正解者に拍手!(平成教育委員会の声)
いかがでしたか?条件付き確率の問題で今回のように「店舗数で加重平均」のようなプロセスをはさんでくるタイプのものは少なくとも通ストレベルではあんまり見ないように思いますが、まあ、簡単簡単。ちゃちゃっと解いちゃいましょう。あと私は陽性/陰性の条件付き確率問題も好きですね、生活密着感あって。
ということで、次回の記事「実際に花子さんをランダムに飛ばして大数の法則を検証」をお待ち下さい。